mctrump · The Insane · 2 points · *
Post reply: https://hugelol.com/lol/997231
Post reply: https://hugelol.com/lol/997261
mctrump · The Insane · 3 points ·
JavaScript is a widely considered a bad programming language due to a combination of multiple types of actions using the same symbols and the fact that it's "stringly-typed". As such, there's a whole bunch of operations where the intended way to them in JavaScript can potentially result in very strange glitches when most programming languages would simply return error messages.
For example, both integer math and string concatenation use the "+" sign as the operator; and if a string is all numbers, then trying to add/concatenate it with a number causes JavaScript to convert one to the other (which is depending on order).
1 + '2' -> 3
'1' + 2 -> '12'
Most other programming languages would error at that, instead demanding that you use functions to convert one type of data to another.
1 + ToInt('2') -> 3
Concatenate( '1' , ToString(2) ) -> '12'
JavaScript is unironically the Dark Souls of programming languages. Git Gud
For example, both integer math and string concatenation use the "+" sign as the operator; and if a string is all numbers, then trying to add/concatenate it with a number causes JavaScript to convert one to the other (which is depending on order).
1 + '2' -> 3
'1' + 2 -> '12'
Most other programming languages would error at that, instead demanding that you use functions to convert one type of data to another.
1 + ToInt('2') -> 3
Concatenate( '1' , ToString(2) ) -> '12'
JavaScript is unironically the Dark Souls of programming languages. Git Gud
Post reply: https://hugelol.com/lol/997277
Post reply: https://hugelol.com/lol/997202
Post reply: https://hugelol.com/lol/997164
mctrump · The Insane · OP · 3 points ·
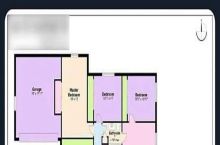
There's a single door to the outside in the living room, and that wall structure between the laundry room and the outdoor bar may be a sliding glass door.
Post reply: https://hugelol.com/lol/997089
Post reply: https://hugelol.com/lol/997102
Post reply: https://hugelol.com/lol/997152
mctrump · The Insane · 6 points ·
 I determined something similar over 5 years ago. Perhaps it is not the outfit, but the woman wearing it.
I determined something similar over 5 years ago. Perhaps it is not the outfit, but the woman wearing it.https://hugelol.com/lol/723029
Post reply: https://hugelol.com/lol/997026
mctrump · The Insane · 6 points ·
That one furry commission I did paid a better rate than my day job.
Post reply: https://hugelol.com/lol/997042
mctrump · The Insane · 4 points ·
They never discard frozen bodies.
What they discard is neither frozen nor does it constitute a body anymore.
What they discard is neither frozen nor does it constitute a body anymore.
Come join us on the unofficial HL Discord server
https://discord.gg/ryFW4M4
 1,004,053
The Insane
1,004,053
The Insane
 1,004,053
The Insane
1,004,053
The Insane Statistics
Joined 10 years ago (2015-11-28 14:48:13).
Has 1,004,053 Karma.
Created 16,887 posts.
Wrote 14,869 comments.
Upvoted 55,834 posts.
Downvoted 19,772 posts.
Achievements Info
Moderator 15.03.2021
Poster of the Year 31.12.2020
The Insane 23.11.2019
7-Year Club 26.08.2025
6-Year Club 03.11.2022
5-Year Club 26.11.2020
Commenter of the Month 30.11.2019
4-Year Club 27.11.2019
Wise 11.09.2019
3-Year Club 27.11.2018
Gold Club 22.09.2018
Poster of the Month x5 31.08.2018
Karma Hunter x10 11.08.2018
Hardcore Commenter 04.08.2018
Hardcore Poster 17.07.2018
Experienced 31.05.2018
Poster of the Day x154 17.01.2018
2-Year Club 27.11.2017
Pepe Collector x7 15.10.2017
Silver Club 24.08.2017
Commenter of the Day x45 17.05.2017
Poster 11.04.2017
Commenter 24.03.2017
1-Year Club 17.02.2017
Verified 15.02.2017
Bronze Club 21.11.2016
Casual Poster 21.11.2016
Casual Commenter 10.09.2016
mctrump's Latest Comments

mctrump · 2 points ·
How to win the supremacy war.
Step 1: Pretend the war is over
Step 2: Convin...

mctrump · 3 points ·
JavaScript is a widely considered a bad programming language due to a combinatio...

mctrump · 2 points ·
 Conceptualization: Easy (Success!)
Schizo Detective
Conceptualization: Easy (Success!)
Schizo Detective
mctrump · OP · 4 points ·

mctrump · OP · 3 points ·
There's a single door to the outside in the living room, and that wall structure...

mctrump · 1 points ·
 Skin theorists having a field day
Skin theorists having a field day
mctrump · 3 points ·
Pay-to-not-play is everyone's favorite game feature :^)

mctrump · 6 points ·
 I determined something similar over 5 years ago. Perhaps it is not the outfit, b...
I determined something similar over 5 years ago. Perhaps it is not the outfit, b...
mctrump · 6 points ·
That one furry commission I did paid a better rate than my day job.

mctrump · 4 points ·
They never discard frozen bodies.
What they discard is neither frozen nor doe...
Step 1: Pretend the war is over
Step 2: Convince the enemy to not fight
Step 3: Psyche
Huh, now that I say it that way, it sounds remarkably like a war crime (false surrender).